2.2. Použité kryptografické principy

Nejdříve si zopakujeme některé kryptografické principy použité v protokolu SSH, konkrétně autentizaci pomocí soukromého a veřejného klíče, zajištění integrity a autentizace přenášených zpráv a protokol Diffie-Hellman pro domlouvání klíčů přes nezabezpečený kanál.

2.2.1. Kód pro ověření zprávy (Message authentication code)

Při posílání zpráv je potřeba zajistit, že nějaký útočník cestou nezmění jejich obsah (zajištění integrity) či místo zprávy nepošle jinou zprávu (zajištění autenticity).

Příjemce zprávy potřebuje poznat, zda ji cestou někdo nezměnil. První, co Vás asi napadne, je vytvoření otisku pomocí kryptografické hašovací funkce. Odesílatel ke zprávě spočítá otisk a zprávu včetně otisku pošle příjemci. Příjemce spočítá z přijaté zprávy druhý otisk a poté oba otisky porovná. Pokud se liší, tak byla zpráva změněna.

Toto jednoduché použití hašovací funkce má vážný bezpečnostní problém. Pokud útočník odchytí zprávu, tak ji může změnit, spočítat svůj otisk a poté upravenou zprávu se svým otiskem poslat příjemci. Tomu budou při kontrole otisky odpovídat přesto, že je zpráva podvržena.

Existuje několik řešení. Jedním z nich je použití sdíleného tajemství (sdílený klíč, sdílené heslo) pro výpočet kódu pro ověření zprávy (MAC, Message Authentication Code).

Často se používá algoritmus HMAC (keyed-Hash Message Authentication Code), který počítá kód pomocí následujícího zjednodušeného vzorce (chybí zarovnání délky klíče i operace xor s klíčem a předdefinovanými konstantami):

\(\mathbf{\text{hash}}(key + \mathbf{\text{hash}}\left( key + message \right))\)

Poznámka

Používá se zdvojený výpočet, neboť u varianty

\(\mathbf{\text{hash}}\left( key + message \right)\)

je hrozbou length extension attack 10 pro hašovací algoritmy MD5, SHA a SHA-2 11. Variantu

\(\mathbf{\text{hash}}\left( message + key \right)\)

by mohl zneužít odesílatel, pokud by našel dvě kolidující zprávy (dvě zprávy se stejným výsledným hašem).

Dokud útočník nezjistí sdílené tajemství, tak jakoukoliv útočníkovu úpravu příjemce detekuje. MAC vedle integrity zajišťuje i autenticitu – zprávu mohl odeslat pouze ten, kdo zná sdílené tajemství. Uvedené schéma není odolné vůči útoku opakováním (replay attack) – útočník může zprávu zachytit a poslat ji ve vhodný okamžik znovu.

Jak si příjemce s odesílatelem domluví sdílené tajemství? Jedna z variant bude popsána v následující části.

2.2.2. Domlouvání klíče přes nezabezpečený kanál (key exchange)

Sdílené tajemství (sdílený klíč, tajný klíč, sdílené heslo) se používá pro ověření integrity a autenticity zpráv a pro symetrické šifrování přenášených zpráv (zajištění důvěrnosti). Na nezabezpečeném přenosovém kanále si lze domluvit sdílený klíč např. pomocí algorirmu Diffie-Hellman z roku 1976:

1. Jedna strana (obvykle server) vygeneruje či vybere z připraveného seznamu velké prvočíslo (\(P\)) 12 a základ logaritmu \((g)\) a oboje pošle druhé straně.

2. Každá strana si nezávisle určí prvočíslo (server \(k_{1}\), klient \(k_{2}\)), které zůstává jejím tajemstvím. Toto číslo je využito jako „soukromý klíč“ pro další výpočty (neplést se soukromým klíčem pro autentizaci).

3. Každá strana si spočítá „veřejný klíč“ dle vzorce \(K = \ g^{k}\text{ mod P}\), tím vzniknou klíče (\(K_{1}{;K}_{2}\)).

4. Obě strany si vymění klíče (\(K_{1}{;K}_{2}\)).

5. Za použití svého „soukromého“ klíče a „veřejného“ klíče si protistrany spočítají sdílený soukromý klíč (\(j\)), který ačkoliv je vypočítán nezávisle každou stranou (serverem a klientem) z opačných soukromých a veřejných klíčů je pro obě strany totožný.

Tabulka 2.1 Domlouvání klíčů u Diffie-Hellman.

Server		Klient
vybere \(P\) a \(g\) vygeneruje náhodný \(k_{1}\) spočítá \(K_{1} = g^{k_{ 1}}\text{ mod P}\)
	server pošle \(P\), \(g\) a \(K_{1}\)
		vygeneruje náhodný \(k_{2}\) spočítá \(K_{2} = g^{k_{ 2}}\text{ mod P}\)
	klient pošle \(K_{2}\)
spočítá \(j = {K_{2}}^{k _{1}}\text{ mod P }\)		spočítá \(j = {K_{1}}^{k _{2}}\text{ mod P }\)

Český Národní bezpečnostní úřad 13 v současné době doporučuje klíče o délce 2048 bitů (stejně velké musí být i prvočíslo), evropská organizace ENISA 14 doporučuje klíče o délce 3072. Používá se též algoritmus Diffie-Hellman nad eliptickými křivkami, kde jsou klíče o řád kratší. V protokolu SSL/TLS se pro domlouvání klíčů používá také šifra RSA, která má problém forward secrecy (blíže v příslušné kapitole).

Zde popsaná verze algoritmu Diffie-Hellman není odolná vůči útoku „muž uprostřed“ (Man in the Middle). V SSH je algoritmus zkombinován s autentizací serveru.

2.2.3. Šifrování s veřejným a soukromým klíčem

Asymetrická šifra pracuje se dvěma klíči \(S\) a \(V\) – první klíč je soukromý (též se označuje jako privátní), druhý veřejný. Názvy klíčů odkazují na obvyklé použití – soukromý klíč by měl majitel bezpečně uschovat pro sebe, veřejný klíč může sdělit komukoliv (i případnému útočníkovi).

Klíče jsou na sobě závislé – vytváří dvojici. Z veřejného klíče nesmí být možné spočítat soukromý klíč v nějakém reálném čase.

Dvojici klíčů lze použít pro šifrování zpráv a pro digitální podepisování.

Při šifrování se použije veřejný klíč \(V\) příjemce zprávy. Zprávu může dešifrovat pouze vlastník soukromého klíče \(S\).

Při digitálním podepisování podepisující (autor) spočítá haš ze zprávy a ten následně zašifruje pomocí svého soukromého klíče \(S\). Každý příjemce zprávy poté může ověřit podpis - spočítá haš ze zprávy a ten následně porovná s hašem, který získá po dešifrování podpisu pomocí veřejného klíče \(V\) podepisujícího. Pokud jsou stejné, tak ověří, že se zpráva cestou nezměnila a současně ověří (autentizuje) autora podpisu (vlastníka odpovídajícho soukromého klíče).

Poznámka

U algoritmu RSA lze použít stejnou dvojici použít pro oba účely, ale nedoporučuje se to. U ostatních algoritmů se pro každý účel generuje samostatná dvojice klíčů s odlišnými charakteristikami. Dvojici klíčů pro šifrování nelze zaměnit za dvojici klíčů pro digitální podpis.

2.2.4. Autentizace serveru

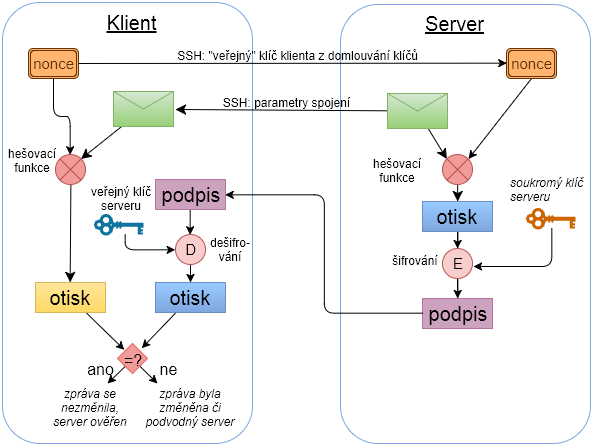
Před zahájením autentizace serveru musí mít server vygenerovánu svoji dvojici veřejný a soukromý klíč a klient musí znát veřejný klíč serveru. Autentizace má poté následující kroky:

1. Klient vygeneruje náhodný řetězec (nonce) a pošle ho serveru. Bez tohoto náhodného řetězce by útočník mohl provést útok opakováním. V případě SSH se jako náhodný řetězec použije „veřejný“ klíč klienta \(K_{2}\) z protokolu Diffie-Hellman (viz předchozí část).

2. Server pomocí hašovací funkce vypočítá otisk z nonce a ze zprávy s dohodnutými parametry komunikace (jaké se budou používat algoritmy).

3. Server otisk zašifruje pomocí svého soukromého klíče a tím vytvoří digitální podpis.

4. Server zprávu a digitální podpis pošle klientovi.

5. Klient pomocí hašovací funkce vypočítá otisk z nonce a ze zprávy.

6. Klient pomocí veřejného klíče serveru dešifruje digitální podpis a získá z něho otisk vypočítaný serverem.

7. Oba otisky porovná – pokud se rovnají, tak se ověřila integrita zprávy, autenticita zprávy a autenticita serveru.

Poznámka

Uvedený průběh autentizace předpokládá, že klient má předem veřejný klíč serveru. Jak klient ověří, že veřejný klíč patří správnému serveru?

Odpověď najdete v následující kapitole.

---

10

viz https://en.wikipedia.org/wiki/Length_extension_attack

11

Útok se týká hašovacích funkcí vytvořených pomocí Merkleovy-Damgårdovy konstrukce. U SHA-3 a některých dalších hašovacích funkcích není zdvojený výpočet nutný.

12

Vygenerování a otestování velkého prvočísla (1024 a více bitů) trvá dlouho (vteřiny až minuty). Proto jsou prvočísla často součástí distribuce serveru, popř. se generují při instalaci programu. Několik konkrétních prvočísel bylo definováno i ve standardech – „Diffie Hellman group 1“ (prvočíslo 768 bitů), „Diffie Hellman group 2“ (1024 bitů) až „Diffie Hellman group 14“ (2048 bitů). Poté stačí poslat protistraně číslo skupiny.

13

Vyhláška o bezpečnostních opatřeních, kybernetických bezpečnostních incidentech, reaktivních opatřeních a o stanovení náležitostí podání v oblasti kybernetické bezpečnosti (vyhláška o kybernetické bezpečnosti) č. 316/2014 Sb.

14

Viz Algorithms, key size and parameters report 2014, dostupné na https://www.enisa.europa.eu/publications/algorithms-key-size-and-parameters-report-2014